Why Is Hexadecimal So Important in Computing? An In-Depth Explanation

Md Sohel Rana in Binary Converters Sep 10 / 7 hours ago

How to Convert Binary to Hex Manually: A Step-by-Step Guide

In a world of instant digital tools, why would anyone bother learning to convert binary to hex by hand? While online converters are indispensable for speed and accuracy, understanding the manual process is a fundamental skill that separates a casual user from a true tech professional. It's the difference between knowing what the answer is and understanding why it's the answer.

This knowledge is a rite of passage for computer science students, a crucial skill for embedded systems engineers, and a powerful tool for any developer who wants to look under the hood of how a computer "thinks." Manually converting binary to hexadecimal demystifies the relationship between these two critical number systems and deepens your understanding of data representation at its most basic level.

This comprehensive guide will walk you through the entire process, step-by-step. We'll cover the core concepts, provide clear examples, and show you the simple logic that makes this conversion possible.

Prerequisites: Understanding the Building Blocks

Before we jump into the conversion process, let's quickly review the essential concepts. A solid foundation here will make the steps ahead incredibly intuitive.

What is Binary (Base-2)?

The binary system is the native language of every computer. It's a base-2 system, meaning it only uses two digits: 0 and 1. Each digit is called a bit. These bits represent the simplest possible states: on/off, true/false, or the presence/absence of an electrical signal. While perfect for machines, long strings of binary are cumbersome for humans to work with.

What is Hexadecimal (Base-16)?

The hexadecimal system is a base-16 system. It uses sixteen symbols: the digits 0 through 9 and the letters A through F (where A=10, B=11, C=12, D=13, E=14, F=15). Its primary purpose in modern computing is to serve as a human-friendly representation of binary code.

The Magic Link: Nibbles and the Power of Four

The reason binary and hexadecimal work so well together is based on a simple mathematical relationship: 24=161.

This means that exactly four binary digits (bits) can be represented by a single hexadecimal digit. This group of four bits has a special name: a nibble. The entire process of manual binary-to-hex conversion is built upon this concept of translating 4-bit nibbles.

The 3-Step Method to Convert Binary to Hex Manually

Once you grasp the concept of the nibble, the conversion becomes a simple three-step process of grouping, looking up, and combining. Let's break it down.

Step 1: Group the Binary String into 4-Bit Nibbles

Take your binary string and, starting from the right-hand side, divide it into groups of four.

Example 1:

Binary String: 1110100101100011

Grouped from the right: 1110 1001 0110 0011

This works perfectly because our string has 16 digits, which is a multiple of 4. But what if it doesn't?

Handling Uneven Strings: Padding with Zeros

If your binary string's length isn't a multiple of 4, the leftmost group will have fewer than four digits. In this case, you simply add leading zeros to the front of that group until it has four digits. This is called padding, and it doesn't change the number's value.

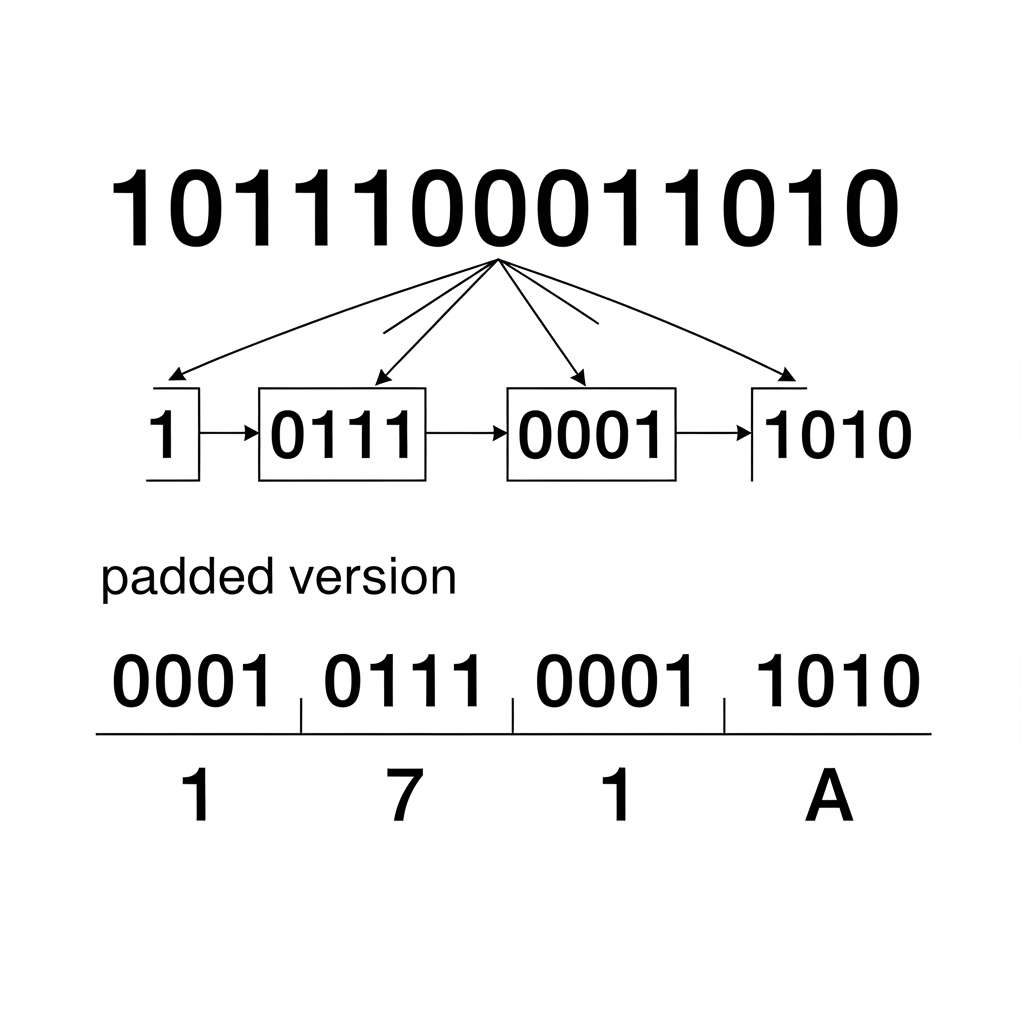
Example 2:

Binary String: 1011100011010

Grouping from the right: 1 0111 0001 1010

The leftmost group is just 1. We need to pad it with three zeros: 0001 0111 0001 1010

Step 2: Use the Lookup Table to Convert Each Nibble

Now that you have your 4-bit nibbles, you'll convert each one into its corresponding hexadecimal digit. You'll need to memorize or reference this simple conversion table.

The Essential Binary-to-Hex Conversion Table:

Step 3: Combine the Hexadecimal Digits

The final step is to take the hexadecimal digits you found for each nibble and write them together in the same order. This forms your final hexadecimal number.

Worked Examples: From Simple to Complex

Let's walk through a few examples to solidify your understanding.

Example A: A Standard 16-Bit String

Let's convert the binary string 1101011100101010.

Group into Nibbles: 1101 0111 0010 1010

Convert Each Nibble:

1101 → D

0111 → 7

0010 → 2

1010 → A

Combine the Hex Digits: D72A

Therefore, 1101011100101010 in binary is D72A in hexadecimal.

Example B: A String Requiring Padding

Now let's convert the binary string 11011101001.

Group into Nibbles (from the right): 110 1110 1001

Pad the Leftmost Group: The leftmost group 110 only has three bits. We add one leading zero to make it a full nibble. 0110 1110 1001

Convert Each Nibble:

0110 → 6

1110 → E

1001 → 9

Combine the Hex Digits: 6E9

Therefore, 11011101001 in binary is 6E9 in hexadecimal.

The Fast and Error-Free Alternative

The manual method is an excellent mental exercise and a crucial concept to understand. However, in a real-world development or networking scenario, speed and accuracy are paramount. A single error in a manual conversion can lead to hours of wasted debugging time.

For this reason, when you need a guaranteed, instant result, using a professional tool is the smart choice. You can try this process instantly with Binary To HEx, a free online tool that converts binary to hex in seconds → https://seomagnate.com/binary-to-hex. It handles all the grouping and padding for you, eliminating any chance of error.

Bonus: The Reverse Process - Hex to Binary Manually

Understanding the process in reverse is just as easy and further solidifies your knowledge. To convert hex to binary, you simply reverse the steps:

Take each hexadecimal digit.

Use the lookup table to find its 4-bit binary equivalent.

Combine the binary nibbles.

Example: Convert 4CF to binary.

Separate the hex digits: 4, C, F

Convert each digit:

4 → 0100

C → 1100

F → 1111

Combine the nibbles: 010011001111

You can drop the leading zero, so the final answer is 10011001111.

Conclusion: A Skill Worth Mastering

Learning to convert binary to hex by hand is more than just a party trick for nerds. It's a foundational skill that gives you a deeper appreciation for the structure of digital information. It strengthens your problem-solving abilities and equips you to understand data at a lower level, whether you're analyzing network packets, debugging code, or simply satisfying your curiosity.

While tools like our Binary To HEx converter are essential for professional efficiency, the knowledge of the manual process behind them will always be valuable.

Frequently Asked Questions (FAQ)

1. Why do we start grouping from the right instead of the left? We group from the right to ensure the correct positional value of the bits. The rightmost bits are the least significant, and any required padding (adding zeros) must be done on the left to avoid changing the number's actual value.

2. What if a binary string contains characters other than 0 and 1? A valid binary string can only contain the digits 0 and 1. If you encounter any other character, the string is not a valid binary number, and the manual conversion method cannot be applied.

3. Is there a limit to the size of the binary number I can convert manually? Theoretically, no. The three-step process (group, convert, combine) works for a binary string of any length. However, for extremely long strings, the process becomes very time-consuming and the probability of making a human error increases significantly.

4. How long does it take to memorize the binary-to-hex conversion table? With a little practice, most people can memorize the 16 values in the table in under an hour. A great way to practice is to start with the easy ones (0000, 0001, 1000, 1111) and then work your way through the others.